人工智能
目前最火的技术莫过于人工智能,或者说机器学习。从IBM Watson到Google AlphaGo,人工智能仿佛已经冲出了实验室,在实际生活中发挥作用。面对如此高大上的技术,普通老百姓要如何去看待它,理解它呢?
首先要知道机器学习的本质是算法,这里就会有好几种,比如:神经网络、支持向量机、朴素贝叶斯等等一堆。虽然算法很多,但他们主要解决的都是同一个问题—分类预测问题。为什么分类预测问题这么重要?因为机器学习的本质是重现人类学习的过程,这个过程可以大致分为两部分:1.定义一个事物,2.判断一个事物。如果一个机器可以对一个事物进行判断,判断的结果与人类的判断相似,那它近似的就是一个人工智能。
假设这样一个场景,我和机器都看到了一个苹果,按照之前对机器的训练如果他告诉我他看到了一个苹果,那说明这个机器是具有一定人工智能的,如果它还能告诉我这个苹果的产地,成熟度,净重,品种、颜色、气味特征等等….我也不会惊讶,因为这是描述一个苹果的特征,也是机器定义这是一个苹果的依据。你看,这里就出现了一个人类与机器的差异,我们学习一个事物并不需要太多维度的特征来描述一个事物,比如,在某某地区生长的、重量在这个范围的、颜色可能是这种的、可能有这些形状的、…(此处省略无限字,因为可以从无限个维度去描述一个苹果),OK,这个东西叫苹果!我们只要摸过吃过看过,大概就知道啥是苹果,也不会和梨搞错,为什么!因为我们聪明,没错,我们的大脑做了定义和判断的工作并且是在我们无意识的情况下。从这个角度上来说,其实研究机器学习的本质其实是研究人类自己认识这个世界的过程。
神经网络
本篇文章的主题就是人工神经网络中的反向传播算法(Back Propagation Algorithm,BP算法)。反向传播算法是实现人工神经网络(Neural Networks,NNs)中非常重要的技术,就是它让神经网络变的“智能”,本文将会利用最简单的NNs模型来模拟整个反向传播算法,并同时使用JavaScript来实现整个过程,文章的最后会提供该例程序。这里需要声明一点,这个程序只是为了演示算法。好了,开始吧。
首先神经网络的模型是这个样子的,这是一个简化到不能在简化的神经网络结构,图中的球模拟了神经元的细胞,线模拟了神经元的突触,简而言之它在用数学模型模拟我们的大脑:

在左侧有i1,i2,表示输入层;最右侧有o1,o2,表示输出层。当我们在训练机器学习的时候,会把输入值和输出值都设定好,好比说,i1=0.15,i2=0.10;计算结果应该是o1=0.01,o2=0.99,如果训练是成功的,那当我输入相同的输入值时,结果应该也是相同的。是不是有点像我们在构造一个函数,而这个函数的计算过程我们并不能看到,这也是为什么很多人说神经网络是一个黑盒模型。我们需要在中间加入一层来描述其中转换的过程,由于是不可见的,这层叫隐含层h1,h2。现在我们需要初始化节点之间的连线,为这些连线加上随机的权值。这些初始化的权值会在之后的计算中被更新,事实上这些权值就是描述这个机器思考的模型。在计算的过程中,我们还会用到b1,b2,这称为偏置项,值永远是1,权值可以自由设置,这里我们设b1权值为0.35,b2权值为0.60。OK,现在这个模型变成了这样:

好了,一切就绪,我们要开始算了!怎么算呢?整个算法的过程分为3个部分:前向传播、计算误差、反向传播,可以理解为我先试一下现在判断,与预期的判断做个比较,然后修正我的判断,下面就每个步骤详细说明一下。
前向传播
首先我们会从模型的左侧计算到右侧,这个方向称为前向。这一步可以分为2步,第1步是简单的加权相加或者叫做线性回归,第2步是代入一个激活函数,激活函数的作用是将线性函数表达为非线性函数,它会把值挤压进一个(0,1)区间的范围作为规范化处理,同时还可以反应出对象的条件概率,激活函数使用sigmoid函数,exp函数表示了以e为底的指数函数:
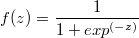
1 | //激活函数 |
第1步,计算线性回归:
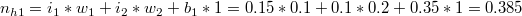
第2步,激活:

现在我们就计算出了h1节点的值,用相同的方法,我们计算出h2,o1,o2节点:
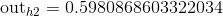
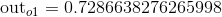
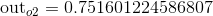
1 | //前向传播 |
可以看到计算的结果和我们设定的结果(0.01,0.99)有很大的误差,这很大程度上是由于权值初始化的时候,接下来我们需要减小这个误差。
计算总误差
误差计算通过平方误差函数为每个节点计算误差,然后将这些误差相加计算总误差:
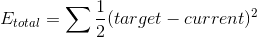
1 | //计算总误差 |
我们分别计算o1,o2的误差值,并将他们相加:
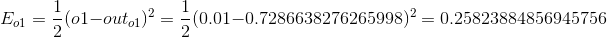
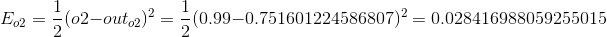
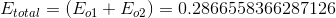
反向传播
现在我们从模型的右侧开始向左侧计算,目标是要使得总误差值变小。我们首先计算w5这一路,这里需要一个方法来计算w5对总误差的影响,刚好导数的意义是描述参数变化对函数造成影响的变化率,或者叫斜率。所以我们想知道w5对总误差带来的变化率可以通过求w5的偏导来计算。然而单纯去算是算不出的,要使用连式法则来分解计算步骤(宏观上看这些中间变量都可以被约分约掉),下面我们就将这个问题分为等式右侧的3部分去求解:
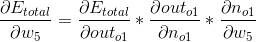
第1部分,o1的输出对于总误差的影响,由于我们不关心o2的输出,所以整个右侧可以计算为0,然后利用求导公式就可以算出:
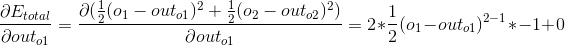
代入之前的数据可以求解:
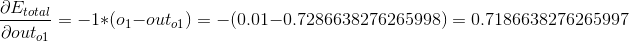
第2部分,这里其实就是对于激活函数来说,o1输出对它的影响,由于激活函数是sigmoid,其求导公式推导如下:
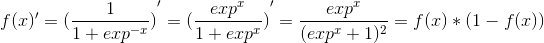
所以我们可以得到第二部分的求解:
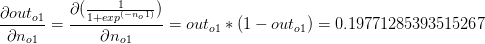
第3部分,w5对于线性方程的影响,其求导结果就是w5的斜率:
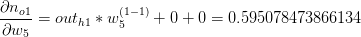
现在!该有的都有了,现在我们知道w5对于总误差的影响有多大了:
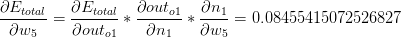
我们现在要对w5这项权值做出调整,调整的依据是刚刚算出的误差值,通过加权的方式去调整,我们需要设定一个学习率来衡量误差对于调整过程的比例,本例中设为0.5:
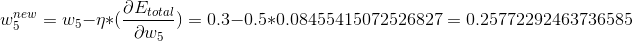
神奇的事情发生了,可以看到w5的权值由原来的0.3调整为0.25772292463736585,从调整的幅度上来看好像还挺有道理的,我们用相同的方法把所有的权值都调整一遍:
1 | //反向传播第一层 |
OK,到目前为止,我们已经成功一半了,接下来需要更新w1~w4的权值,以w1为例,我们需要算出w1对于总误差的影响,依然通过链式法则求偏导:
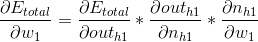
这里有一个情况出现了,我们的算式里第一项是描述h1节点对于总误差的影响,如何描述这个影响,直接求求不出啊?冷静,思路依然是将问题细分,我们可以看到模型中这个h1节点可以影响o1,也可以影响o2,所以这个过程可以看做h1对o1,o2的影响之和,下面我们开始计算:
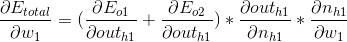
第1部分,这一部分其实又可以分为2个小部分,我们以计算o1例。在计算的时候有一个技巧,o1输出对于E0的影响其实就等于o1输出对于E_total的影响,所以可以用之前算过的值直接代入;由于out_o1是线性方程,h1对于out_o1的影响就等于其斜率w5:
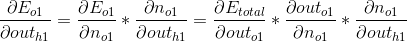
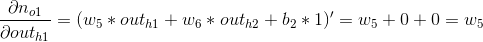
代入之前求得的值就可以求解第1部分:
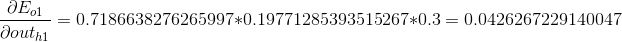
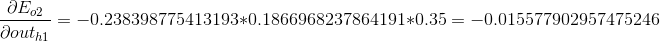
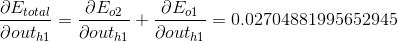
第2部分,就是对sigmoid函数求导,代入可以求解:
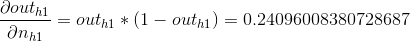
第3部分,是对线性函数求导,求解:
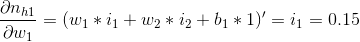
大功告成,我们将3部分数据相乘,并加上学习率,最终求解:
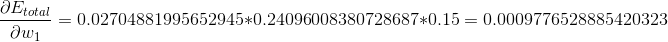
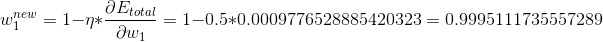
我们将其余的权重都求解:
1 | //反向传播第二层 |
目前为止,我们已经完成了训练,接下来我们来验证一下训练的成果。仍然将[0.15,0.1]作为输入层输入,我们看到通过新的权重计算后得到的结果是:1
预测值变化:0.7286638276265998,0.751601224586807 => 0.7185477013468267,0.7545430129300831
可以观察到o1越来越接近0.01,o2越来越接近0.99,OK,我们来循环10000次,观察训练后的结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14var test = new Neural();
var final_o=[];
for (var i = 0; i < 10000; i++) {
test.forward();
var old_o=[].concat(test.o);
test.totalError();
test.backward1();
test.backward2();
test.forward();
final_o=[].concat(test.o);
}
console.info('最终预测值:'+final_o);
-----------------------
最终预测值:0.015360963767399535,0.9845412722122693
最终结果已经非常接近我们的预期值。但是这里如果一味的增加训练次数会产生边际效应,最终的预测值会越来越慢的接近目标值。
结语
最终我们模拟了最为简单的神经网络结构,可以想像如果增加输入层维度,并且增加隐含层层数,模型的拟合度会越来越高,计算量也会指数倍增长。
本例代码:https://github.com/yuri147/hexo/blob/master/source/js/bp/bpdemo.js